Janos Perczel

Theoretical Quantum Physics

Part III of the Mathematical Tripos, Applied Mathematics

Logic, Philosophy of Science and Physics

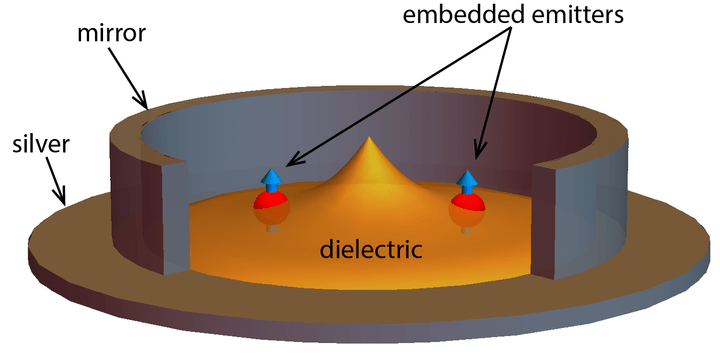
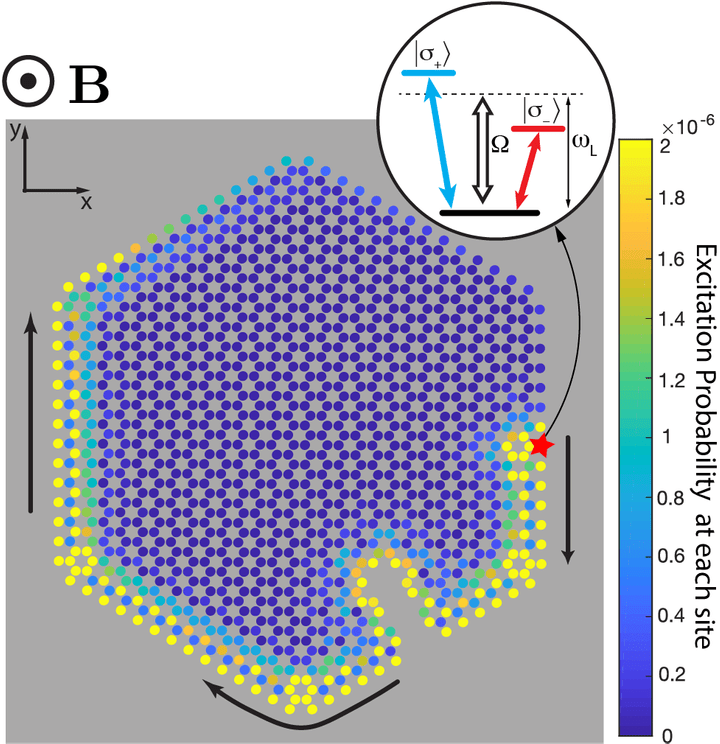
In this work, we proposed a novel nanophotonic platform that creates strong interactions between atomic bits (qubits) and visible-frequency photons and gives rise to robust photonic states that are extremely resistant to imperfections, such as missing qubits and noise. Such states are important for creating topological quantum computers.

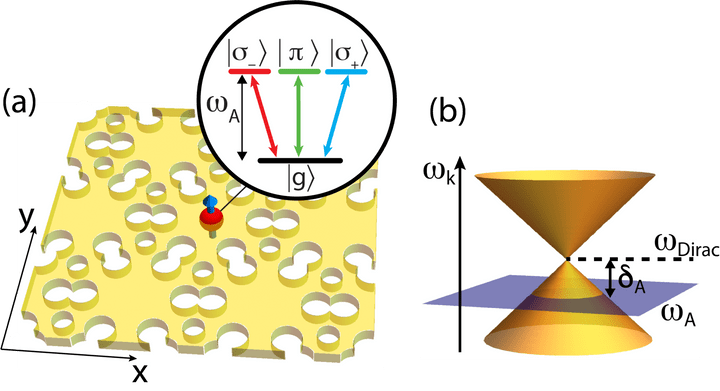
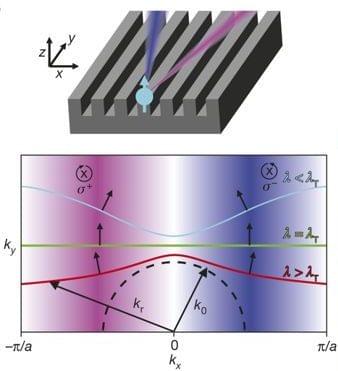
In this paper, we developed a mathematical and computational framework to describe the light emitted by a single atom near a nanophotonic structure with a so-called Dirac cone spectrum. Such photonic structures are actively explored for building large-scale quantum networks,

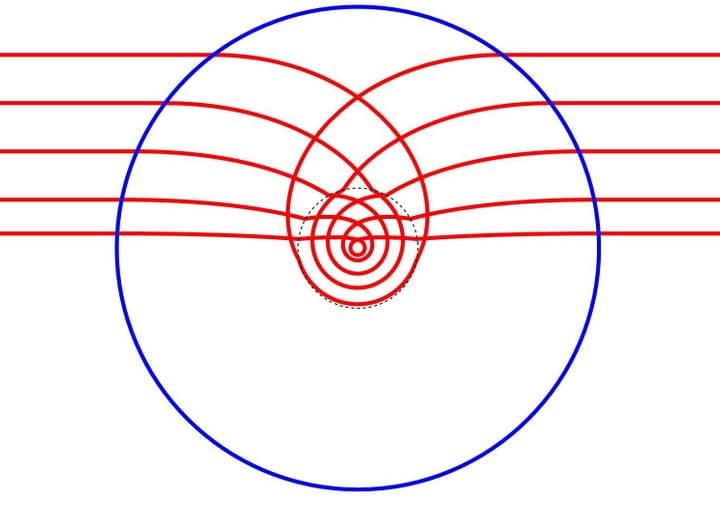
In this work, we resolved a long-standing controversy regarding the focusing abilities of an optical lens, called Maxwell's Fish Eye. We showed that the lens cannot focus photons to an area whose diameter is smaller than the wavelength of light. We also demonstrated that this lens can create 'entanglement' (the most valuable quantum resource) between atoms.

In this project, we showed that that 2D atomic lattices suspended in free space using lasers can trap visible-frequency photons and guide them around in lossless circular orbits even in the presence of significant imperfections.

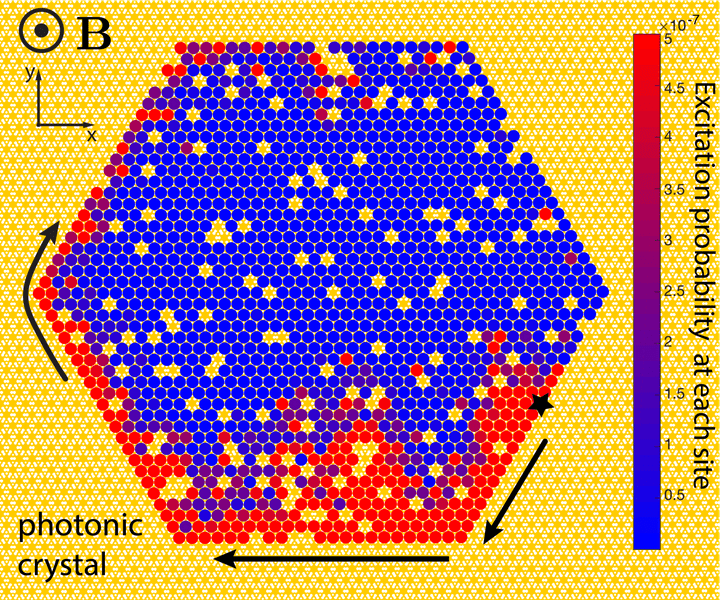
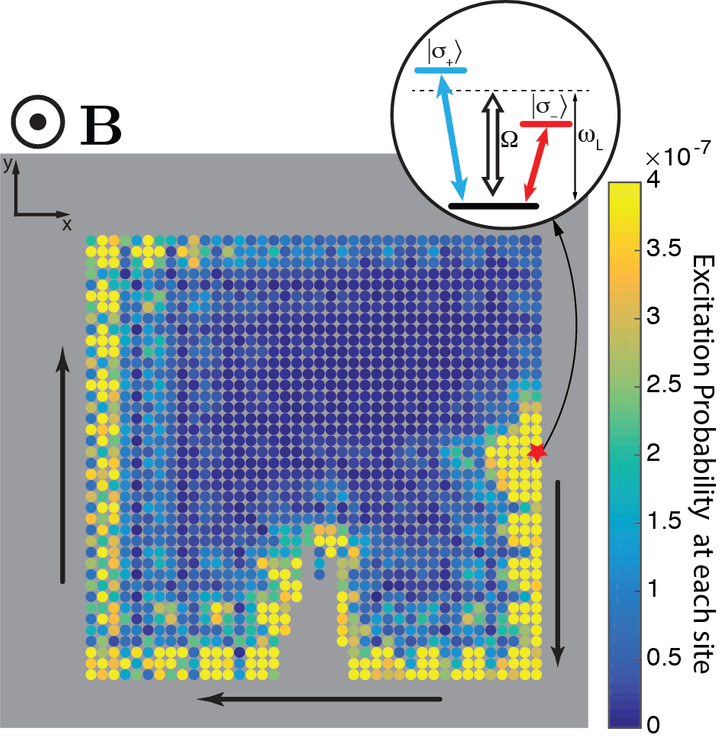
In this paper, we borrowed ideas from an abstract branch of mathematics, called topology, to design an atomic system, where photons can travel around the edges of an atomic system with little to no sensitivity to imperfections and missing atoms.

In this experimental project we showed that a non-sized silver grating can exhibit the so called spin-orbit coupling of light, which has important applications in quantum information processing. 

In this paper, we provided the theoretical blueprint for an invisibility cloak that can make objects invisible regardless of their color. Previous proposals for invisibility cloaks were all functional only at a single frequency (i.e. single color).  

In this work we showed that the invisible sphere (an invisible optical lens) can be implemented with physical parameters that require very careful engineering only in a limited region of the lens (near the center of the sphere).  

In this project, we showed how Non-Euclidean geometry can be used to design a system that can hide objects from sight without requiring extreme material parameters for implementation.